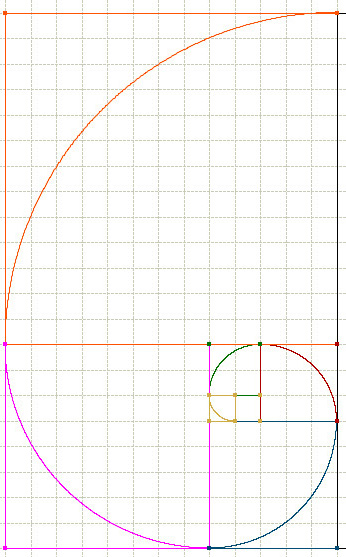Champs : 3- Rues de Pondichéry |
||||||||||||||||||||||||||||||||||
|
1ère partie : suite de KOLAM (1), KOLAM (2) et KOLAM (3) : (en cours) Ces quelques illustrations font apparaître plusieurs significations des kolam que l'on peut résumer ainsi : [Nous rappellerons ici, pour mémoire, quelques données pouvant être mobilisées pour l'interprétation des kolam, touchant : - la signification de la symétrie, - du motif de la spirale, - du labyrinthe, - de la droite et de la gauche. Elles font apparaître la relation de la main et du calcul dans la pénétration et dans la célébration des formes.] Le motif du labyrinthe Cognitionem aggressuro, quam Thesei filum labyrinthum ingressuro. Une difficulté touchant l'interprétation des kolam par le modèle du labyrinthe (ou de la spirale vue comme une figuration de l'accès au centre), c'est que les kolam se singularisent plutôt par le caractère eulérien (fermé) de leur parcours (une progression sans fin qui ramène nécessairement au point de départ),
École de Leonardo Vinci quand la progression dans le labyrinthe comporte un point de départ et un point d'arrivée (difficilement accessible). "Le labyrinthe est, essentiellement, un entrecroisement de chemins, dont certains sont sans issue et constituent en fait des culs-de-sac, à travers lesquels il s'agit de découvrir la route qui conduit au centre de cette bizarre toile d'araignée. La comparaison avec la toile d'araignée n'est pas exacte d'ailleurs, car celle-ci est symétrique et régulière, alors que l'essence même du labyrinthe est de circonscrire dans le plus petit espace possible l'enchevêtrement le plus complexe de sentiers et de retarder ainsi l'arrivée du voyageur au centre qu'il veut atteindre." (Brion, Marcel, Léonard de Vinci, 1952 : 197)
Le labyrinthe représente le cheminement vers le centre caché, imprenable (comme l'exprime la figure ci-dessus) ; il est plus généralement le symbole du cheminement initiatique, de l'élucidation de la complexité et du triomphe sur l'obscurité, mais aussi de la sortie, de l'évolution et de l'involution, de la pénétration et de la libération. (Ainsi cet Abhyumani yantra : pour délivrer une parturiente, on lui fait boire de l'eau safranée ayant parcouru un labyrinthe dessiné sur un plateau.) Eh bien figurez-vous que l’intérieur de ce morceau de gruyère n’était pas banal. Ça n’arrêtait pas de tourner en rond. Il fallait faire au moins dix mètres pour progresser d’un mètre vers le centre ! Cela ressemblait à la file d’attente en escargot de Disneyland, quand on fait la queue pour le “Train fou”. Pour donner aux clients l’illusion d’être tout près du but, on les entasse à quelques mètres de l’entrée sur la plus petite surface possible tout en les faisant avancer le long de la main courante spiralée... qui n’en finit pas...; aurait-on la patience d’attendre son tour si l’on déroulait cette file désespérante ?... Bon. Tout ça pour dire que le labyrinthe, c’est pas seulement un truc pour faire patienter les gogos. Cela sert aussi à égarer ceux qui croient qu’une route est faite pour conduire quelque part, pour dérouter les jobards gobeurs de bobards qui s’engouffrent sans réfléchir au premier détour. Donc à force de virer, nos trois gaillards commençaient à avoir le tournis dans leur morceau de fromage. Partis bille en tête et ventre à terre, sans ce fameux fil d’Ariane qui met du sens dans les divagations, ils commençaient à se poser des questions. [...] http://philantropiques.free.fr/contesenligne.data/Composants/estceque.html La symétrie La généralisation qui conduit de la symétrie bilatérale à la symétrie au sens plus large de la géométrie (opération mentale dont on peut chercher des exemples dans la nature) consiste à substituer à la réflexion par rapport à un plan un groupe quelconque d'automorphisme. Le cercle de centre O dans un plan, puis la sphère de centre O dans l'espace, possèdent ainsi la symétrie décrite par le groupe de toutes les rotations autour de O, dans le plan ou dans l'espace respectivement. La symétrie bilatérale est une opération à une dimension. La symétrie cyclique apparaît dans sa forme la plus simple dans un plan perpendiculaire à l'axe. Les fleurs illustrent ce type de symétrie, la plus fréquente mettant en œuvre le chiffre 5. Dans un espace à trois dimensions, le mouvement d'un solide est un mouvement en forme d'hélice qui associe une rotation autour d'un axe et une translation parallèle à cet axe. (Cf. la remarque d'Héraclite : la vis conjugue le mouvement circulaire et le mouvement rectiligne.) La croissance végétale – la foliation, par exemple – emprunte fréquemment (plantes spiralées) cet agencement qui paraît répondre aux conditions optimales d'exposition. Les pétales apparaissent alors à la terminaison du parastiche (voir infra).
La gravité et le mouvement La nature paraît en effet presque universellement soumise à la symétrie. La gravité y est pour quelque chose : l'état d'équilibre n'étant rien d'autre qu'une symétrie. Une masse de matière quelconque doit prendre une forme sphérique autour de son centre : c'est généralement le cas des organismes en suspension. "Dans les fluides mêmes, note Leibniz dans les Nouveaux Essais (II, 4, De la solidité), il y a de la cohésion ordinairement, comme les gouttes d'eau et de mercure le font voir". Alors que la symétrie radiale est associée à la sédentarité d'espèces fixées à un substrat, comme l'oursin (elle offre une orientation optimale), les êtres vivants doués de mobilité développent une symétrie relative à la gravité et au milieu. La symétrie bilatérale, l'aérodynanisme, qu'on observe chez les vertébrés résulte de cette ingénierie de la mobilité dans un milieu donné. Pour distinguer un mammifère marin d'un poisson, il suffit d'observer le plan de la nageoire caudale : il est horizontal chez le premier et vertical chez le second. Le "plancher des vaches" constitue le plan résistant, support de la locomotion des mammifères qui engage l'ondulation de la colonne vertébrale dans le plan vertical. Les mammifères qui sont retournés à l'eau ont conservé cette caractéristique acquise sur la terre ferme. La fluidité du milieu aquatique permet, lui, une ondulation de la colonne vertébrale dans divers plans, notamment et principalement dans le plan horizontal de la locomotion. La configuration de l'enveloppe corporelle est un compromis entre l'identité de l'organisme en mouvement, son invariance morphologique, et le milieu. Quand il y a asymétrie chez les vertébrés, elle est intérieure. La direction du déplacement détermine un axe antéro-postérieur, une gauche et une droite. Les côtés droit et gauche se développant sous le contrôle de gènes régulateurs (gènes de la famille Hox qui jouent un rôle comparable chez nombre d'animaux et de végétaux), l'asymétrie phénotypique est généralement déviante. Prenant au mot la fable que Platon prête à Aristophane dans le Banquet et la menace que Zeus fait peser sur les hommes d'aujourd'hui (s'ils s'avisaient de mettre de nouveau en cause la souveraineté des Olympiens qui leur a valu cette rétrogradation de la symétrie radiale qui leur conférait une force extraordinaire, à la symétrie bilatérale – notre condition d'aujourd'hui), il faut bien imaginer une réparation qui réorganiserait la symétrie perdue de ce quart condamné à courir après son quart avant de retrouver sa moitié... De la roue (l'androgyne tétrascèle primitif) à la croix : Symétrie et chiralité : l'inorganique et l'organique La symétrie naturelle inspire la main de l'homme quand il crée, mais aussi sa spéculation quand il cherche à comprendre les voies de la nature. L'observation empirique rencontre ici l'observation scientifique. Les exemples de symétrie les plus frappants sont donnés par les cristaux et ce sont les expériences de Pasteur sur l'acide racémique (à l'origine de la stéréochimie) qui lui firent penser que la formation de composés optiquement actifs (provoquant une rotation angulaire du plan de polarisation de la lumière) était la prérogative de la vie : "C'est peut-être la seule ligne de démarcation nette qu'on puisse à présent tracer entre la chimie de la matière morte et celle de la matière vivante". Depuis les travaux de Pasteur sur les tartrates, on sait que tous les corps doués du pouvoir rotatoire sont susceptibles d'exister sous deux formes, l'une dextrogyre, l'autre lévogyre, deux "antipodes optiques" aux propriétés (physiques) identiques, à ceci près que l'une dévie la lumière polarisée à droite et l'autre à gauche. (L'association des deux antipodes en proportions égales n'a plus aucun pouvoir rotatoire, et leur mélange – dit racémisation, en mémoire de Pasteur – établit la symétrie qui manquait à chacun d'eux.) Pour illustrer la chiralité, Pasteur proposait (à l'instar de Kant, infra) de comparer la structure moléculaire des antipodes optiques à un objet et à son image réfléchie dans la glace ou encore aux deux mains, la droite et la gauche, "qui sont bien constituées par le même nombre de doigts, mais disposés en sens inverse, symétriques et non superposables. Pour accoler les deux mains, il faut les retourner l'une par rapport à l'autre : c'est alors qu'elles se joignent exactement, et leur ensemble forme un groupement symétrique, symétrique par rapport au plan de leur accolement, à l'instar d'un couple racémique. Pasteur insiste sur le fait que toutes les substances à dissymétrie moléculaire sont, sans exception et à la différence des "produits artificiels" élaborées par le vivant. C'est à la matière vivante, et à elle seule, qu'est réservé le privilège d'imprimer à une substance le caractère dissymétrique, et cela parce que la matière vivante est elle-même affectée d'une dissymétrie qu'elle propage. "Il semble donc bien que, dès les origines mystérieuses de la vie, la matière vivante se soit trouvée marquée d'une dissymétrie originelle dont la cause nous échappe et qui se transmet en héritage à travers les siècles des siècles. Il n'y aurait pas plus de synthèse asymétrique spontanée que de génération spontanée ; la première synthèse asymétrique ne serait pas plus expliquée que l'origine du premier germe vivant." (citation de : http://www.lc-maillard.org/biog15.htm, centenaire de Pasteur) Dans les organismes vivants, en effet, les protéines sont exclusivement constituées d’acides aminés de type "gauche". Cette sélection d'une seule des deux symétries est une énigme scientifique à laquelle cristallographes, chimistes et biologistes tentent de répondre. Les propriétés chimiques des éniantomères peuvent, de ce fait, être très différentes. Les formes lévogyres et dextrogyres de l'acide lactique, du propanol, du L-Dopa (précurseur de la dopamine), de l'asparagine, de la thalidomine ou des phéromones, par exemple, ont des effets différents – l'affaire de la thalidomine ayant dramatiquement fait prendre conscience de l'importance de la stéréochimie pour la compréhension des interactions moléculaires. Pour qu'une structure soit chirale, elle doit être dissymétrique (mais non asymétrique). La chiralité implique l'absence : Les spéculations religieuses et sur la signification de la droite et la gauche sont anciennes et probablement universelles. Cette signification est bien entendu liée à la position de l'homme dans l'espace. La discrimination de la gauche et de la droite est liée à la symétrie bilatérale du vivant et à l'opposition antéropostérieure. Mathématiquement, la droite et la gauche sont indiscernables, comme Leibniz l'a montré dans sa discussion avec le pasteur Clarke qui, en disciple de Newton, suppose une réalité de l'espace que Leibniz récuse : l'espace n'est rien sans les corps qui l'emplissent. L'espace est défini mathématiquement par des relations de base, des bijections (transformations biunivoques) entre des points. Dans cet espace, gauche et droite sont relatifs. Mais la vie, précisément, si l'on interprète ainsi la dissymétrie originelle de la matière vivante, visée plus haut, transmise de génération en génération, est orientée. La propriété chirale que déploie la mathématique du vivant exprime aussi l'inclusion de l'homme dans la procession des êtres. "Des différences qui tiennent au fondement même de notre nature sensible" Si deux choses sont parfaitement identiques pour tout ce qui en chacune peut être connu en soi (dans toute détermination, se rapportant à la quantité ou à la qualité), il s'ensuit forcément que pour tous les cas et sous tous les rapports l'une peut se substituer à l'autre sans que de cette substitution puisse résulter la moindre différence appréciable. [...]
Kant, Prolégomènes à toute métaphysique future, pp. 48-49 (1783, ed. Vrin, 1968)
Quelle ressemblance plus parfaite que celle de nos deux mains! Et pourtant, quelle inégalité plus criante ! À la main droite vont les honneurs, les désignations flatteuses, les prérogatives : elle agit, elle ordonne, elle prend. Au contraire, la main gauche est méprisée et réduite au rôle d'humble auxiliaire : elle ne peut rien par elle-même ; elle assiste, elle seconde, elle tient. La main droite est le symbole et le modèle de toutes les aristocraties, la main gauche de toutes les plèbes. Quels sont les titres de noblesse de la main droite ? Et d'où vient le servage de la gauche? Robert Hertz, "La prééminence de la main droite. Étude sur la polarité religieuse", in Sociologie religieuse et folklore.
"Symétries perdues" ? [à développer]
kolam reconstitué : On trouve sur le Net un générateur automatique de kolam, intitulé : "Random Symmetrical Kolam Generator", à l'adresse URL :
Y a-t-il une antériorité ou une supériorité de la ligne qui enferme les points d'un seul mouvement (théorique) de la main ? C'est l'avis de P. Gerdes (1989) [à développer] La spirale
(Lorsqu'on emmène le mort au tombeau, ceux qui portent la civière font des crochets et des demi-tours afin que le mort ne retrouve pas le chemin du village, voir, à la rubrique "Ethnographie de Madagascar" le film Zafimahavita.)
Les dessins sur le sable au Vanuatu, qui sont les productions les plus proches des kolam, sont interprétées par les informateurs de leur découvreur, A. Bernard Deacon, comme la figuration d'une marche vers l'immortalité. Un esprit femelle dessine sur le sable une figure géométrique et, quand l'âme du mort approche, il en efface la moitié. Le mort doit compléter le dessin et marcher sur la forme ainsi complétée pour accéder au pays des morts. Le motif de la spirale fait l'objet de spéculations mystiques de la préhistoire jusqu'à nos jours. A divers titres elle représente ou le voyage de l'âme après la mort ou l'expression du "corps astral" des occultistes.
Les recherches sur les formes géométriques et leur expression numérique ou algébrique nourrissent à la fois, de la préhistoire à nos jours, la recherche scientifique et les spéculations mystiques... Quand j'étais questeur, j'ai découvert [le tombeau d'Archimède] que les Syracusains ignoraient ; ils affirmaient même qu'il n'existait point. Je l'ai découvert entouré et recouvert entièrement de ronces et de buissons. Je connaissais quelques petits vers dont j'avais appris qu'ils étaient inscrits sur sa tombe. Ceux-ci faisaient connaître qu'en haut du monument il y avait une sphère avec un cylindre. Or, en parcourant des yeux toutes les tombes, qui sont très nombreuses à la sortie d'Agrigente, j'aperçus une petite colonne qui émergeait à peine des buissons, sur laquelle se trouvaient les figures d'une sphère et d'un cylindre. Aussitôt je dis aux notables syracusains qui se trouvaient à mes côtés qu'à mon avis c'était là précisément la tombe que je cherchais. Plusieurs hommes, venus avec des faux, débroussaillèrent l'endroit. Une fois le lieu dégagé, nous nous approchâmes du soubassement qui nous faisait face. L'épigramme apparut avec la fin des vers rongée presqu'à moitié. C'est ainsi que la plus illustre cité de la Grande Grèce, jadis même la plus savante, aurait ignoré le tombeau de son concitoyen le plus intelligent si un homme d'Arpinum ne le leur avait pas révélé.
spira mirabilis
Une plaque commémorative apposée sur un des murs du cloître qui jouxte la cathédrale de Bâle à la mémoire de Jacques Bernoulli (1654-1705) qui, dans ses recherches sur les courbes consacra une étude à la spirale logarithmique, porte la formule "Je ressuscite identique à moi-même". En conférant une valeur religieuse aux remarquables propriétés d'invariance de cette spira mirabilis (ainsi qu'il propose de l'appeler), Bernouilli se place sans doute sous le patronage d'Archimède qui aurait fait graver sur son tombeau – que Cicéron raconte avoir découvert alors qu'il était questeur à Syracuse (vide supra) – un cylindre circonscrit à une sphère, mais il se situe aussi dans la continuité des spéculations anciennes sur la valeur mystique des formes remarquables. (Malencontreusement, comme on le voit sur cette photographie, la plaque commémorative de Bernouilli est ornée, non pas d'une spirale logarithmique, mais d'une spirale d'Archimède, la distance entre chaque spire étant identique... Il doit s'en retourner dans sa tombe.) Les Epeires, géométrie de la toile La spirale logarithmique décrit un nombre sans fin de circuits autour de son pôle, dont elle se rapproche toujours sans pourvoir y parvenir. Ce point central, à chaque tour plus voisin, est indéfiniment inaccessible. [...] L'Épeire se conforme de son mieux à cette loi de l'enroulement illimité. Les tours de spire se serrent d'avantage l'un de l'autre en se rapprochant du pôle. A une certaine distance, brusquement ils s'arrêtent ; mais alors fait suite au fil la spirale auxiliaire, non détruite dans la région centrale, et l'on voit, non sans quelque surprise, celle-ci continuer d'avancer vers le pôle en tours de plus en plus serrés, à peine discernables. Ce n'est pas, bien entendu, la rigueur mathématique, mais une approximation très nette de cette rigueur. L'Épeire cerne son pôle de plus en plus près, autant que le lui permet son outillage, défaillant comme le nôtre. On la dirait versée à fond dans les lois de la spirale. [...] Jacques Bernouilli, à qui la géométrie doit ce magnifique théorème, fit graver sur sa tombe, comme un de ses beaux titres de gloire, la spirale génératrice et sa pareille engendrée par le déroulement du fil. Une inscription disait : Eadem mutata resurgo, je ressuscite identique à moi-même. Difficilement la géométrie trouverait mieux que cette superbe envolée vers le grand problème de l'au-delà.
La phyllotaxie se donne pour objet de rendre compte de ces étonnantes réalisations naturelles qui paraissent obéir à un dieu géomètre (Dum Deus calculat fit mundus, disait Leibniz), révélant la soumission des processus de la génération aux contraintes biomécaniques et aux lois de l'équilibre. La célèbre suite de Fibonacci est faite d'une progression de nombres dont chaque terme, à partir du 3ème, est la somme des deux précédents : En calculant les valeurs approchées des quotients de deux nombres successifs de la suite de Fibonacci on obtient : (soit : Un + 1 / Un converge vers (1 +
Ammonite fossile de Madagascar (coll. privée)
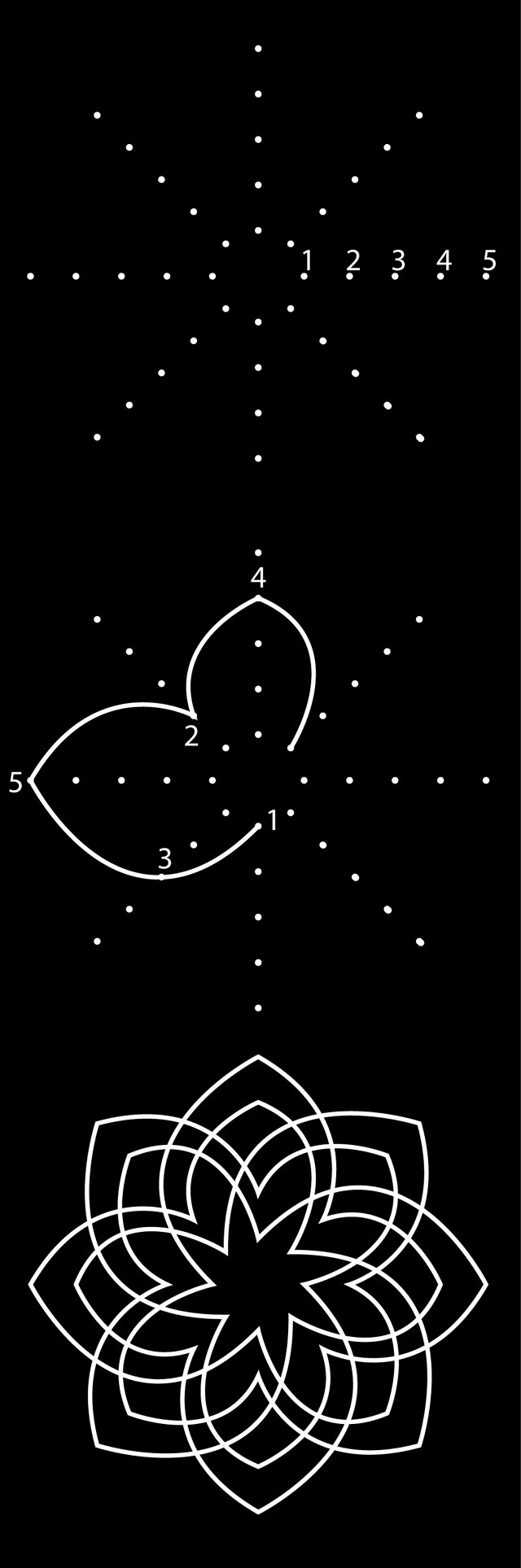
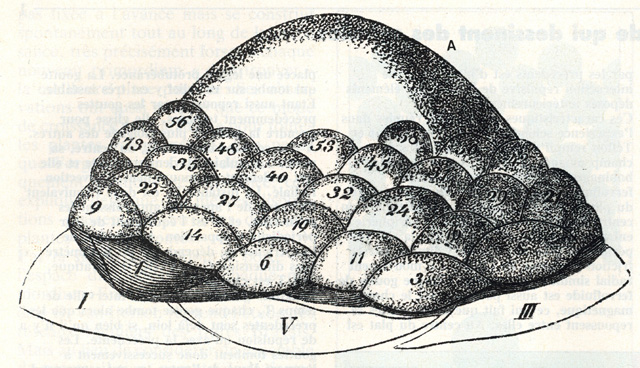
L'organique et l'inorganique : la symétrie pentagonale Un système physico-chimique inorganique aboutit à des états d'équilibre qui se manifestent par des figures géométriques régulières. C'est le cas des cristaux, caractérisés par une symétrie hexagonale. La symétrie hexagonale correspond à un équilibre inerte, sans orientation privilégiée dans le plan et dans l'espace. Cette configuration, qui constitue le mode d'occupation maximal d'une surface ou d'un volume donné (les unités sphériques, comme les bulles ou les alvéoles des ruches s'"empilent" ou se juxtaposent en se résolvant en hexagones circonscrits), se rencontre notamment dans les systèmes où l'engendrement des cellules est soumis aux forces de la capillarité. La vie, comme l'art, mettent en œuvre une dialectique de la symétrie et de la dissymétrie. "Rien ne serre le cœur comme la symétrie, écrit Hugo. C'est que la symétrie, c'est l'ennui et l'ennui est le fond même du deuil" (Les Misérables, Deuxième partie, Cosette, 1863, p. 320). La symétrie – par ailleurs si remarquable, même quand elle est répétitive et "mortelle" – est un résultat adaptatif. Mais la dissymétrie est aussi au cœur de la vie. Les hélices de l'ADN tournent dans le même sens chez tous les êtres vivants. L'art, consiste aussi à rendre la dissymétrie par la symétrie, comme on peut le voir en comparant, par exemple, les parastiches d'une fleur et la mosaïque romaine reproduite plus haut. Ou la symétrie par la dissymétrie, comme le montre le kolam type fleur de lotus (déjà représenté) dit Hridaya Kamalam kolam ("cœur de lotus"). Ce kolam s'effectue d'un seul trait, soit à main levée en suivant le principe "grand pétale/petit pétale", dessinés sur les huit rayons imaginaires de la fleur (hypothèse avec 16 pétales distribués sur deux cercles), soit avec une grille préalable qui matérialise les rayons (chaque rayon = 5 pulli) en suivant le cheminement 1, 3, 5, 2, 4. La ligne dessine de manière continue deux cycles de huit pétales et une étoile de huit branches .
En 1868, le botaniste Wilhelm Hofmeister montre, dans son manuel de physiologie végétale (1868 : 405), qu'à la périphérie de la partie centrale du bourgeon, l'apex, se développent des protubérances, les primordia, qui croissent en s'éloignant du centre (illustration infra) selon une structure spiralée caractérisée par un angle de divergence constant. Les primordia les plus anciens sont les plus éloignés de l'apex et constituent des éléments différenciés. Les cellules se multiplient de telle manière que l'extrémité du bourgeon croît tout en conservant une forme identique. Eadem mutata resurgo. Pour expliquer cette disposition, Hofmeister suppose l'activité d'une règle mécanique simple selon laquelle la position de chaque nouveau primordium est fonction de l'espace libre laissé par les deux précédents. (Cette règle serait générale aux trachéophytes – ou plantes vasculaires.) Cette hypothèse a été vérifiée expérimentalement par Stéphane Douady et Yves Couder (1993) selon le dispositif suivant : des gouttes d'un liquide magnétique (ferrofluide) tombant régulièrement dans une vasque traversée par un champ magnétique. Les gouttes s'éloignent vers le bord et se repoussent entre elles, produisant une structure spiralée.
La géométrie des kolam n'entend évidemment pas reproduire les étapes de la morphogenèse. Comme on le voit avec l'exemple du lotus, c'est la composition finale qui est reproduite. Mais sa rationalité, son économie de moyens tendent vers une formalisation qui n'est pas seulement fondée sur l'analogie (terminale). La symbolisation recherchée se déploie en suivant la grammaire des formes. Les lois de l'esprit rencontrent et réfléchissent les lois de la nature. * Références : - Ascher, Maria, 2002, Mathematics Elsewhere, Princeton, Princeton University Press. Introduction : Frag Présentation : Planches : Galeries :
|
|||