|
Chapitre 18
Plan du chapitre :
A) Le territoire de la langue : les deux natures
Communication présentée au colloque international Langues et droits, Université de Paris X-Nanterre, 22-23-24 octobre 1998.
B) La mesure du monde : Eratosthène et Ptolémée
Communication présentée à la “Journée de l’Antiquité”, Université de la Réunion, 27 avril 2005.
C) “Deux vérités ne peuvent être contraires" (Galilée) (en cours)
D) “Foi d'animal” : vérité du bestiaire dans la fable et le conte
Communication présentée aux “Journées de la Recherche” du CRLHOI, séance du 11 février 2006.
B)
La mesure du monde : Eratosthène et Ptolémée
IV - 18.2
Je souhaiterais d’abord limiter le propos annoncé par le titre de cette communication : non pas “d’Ératosthène à Ptolémée”, mais : “Ératosthène et Ptolémée”. En effet, d’Ératosthène à Ptolémée cela fait près de cinq siècles et beaucoup de monde… (Appolonios de Perge, Philon de Byzance, Cratès, Hipparque, Géminos, Vitruve, Agrippa, Nicomaque, Cléomène… pour citer les principaux noms). Je me bornerai à dire quelques mots, en réalité, d’Ératosthène, d’Hipparque et de Ptolémée…
En cette “Journée de l’antiquité”, j’aimerais commencer par parler d’actualité. Je vais même faire un peu d’anticipation puisque je vais faire état d’un article qui va paraître le mois prochain dans le Journal for the History of Astronomy (May 2005). Cet article traite de l’identification des constellations contenues dans un ouvrage disparu d’Hipparque, astronome grec ayant vécu à Rhodes au deuxième siècle avant notre ère, découverte faite, non pas dans une source manuscrite mais, plus étonnant, sur une statue.
Pour situer Hipparque, qui fait l’objet de cette découverte, probablement la figure majeure de l’astronomie grecque, entre Ératosthène et Ptolémée, je vais citer ce que Pline en dit, pour avoir su prédire, sur plusieurs siècles, les éclipses de la lune et du soleil : “La suite des temps, écrit Pline, a témoigné qu’il n’eut pas mieux fait s’il avait pris part aux décisions de la nature. Grands hommes qui vous êtes élevés au-dessus de la condition humaine en découvrant la voie que suivent les divinités […] salut à votre génie, interprètes du Ciel, vous dont l'esprit embrasse la nature entière, créateurs d’une science qui vous a permis, en décryptant et en révélant les calculs des dieux, de vous arracher à l'esprit misérable et craintif des mortels !” (Histoire naturelle, II : 53-54).
Je vais revenir à Hipparque dans un instant et emprunter, au passage, à Pline le propos de cette communication :
Les “calculs des dieux” sont hors de la portée de nos esprits “misérables et craintifs”. Certes. En revanche, les mathématiques élémentaires sont accessibles à tous. Et je vais me borner à rappeler par quels calculs, d’une géniale simplicité, et par quelles représentations les savants grecs ont réussi à donner une représentation du monde qui a, pour partie, servi de fondement à la science moderne.
En ces temps de “papolâtrie” (la nature même nos esprits “misérables et craintifs” y est probablement pour quelque chose), j’aimerais aussi poser la question de savoir pourquoi (je n’ai pas de réponse à proposer ici) le “fénoir” de la théologie chrétienne a pu, pendant dix siècles, ignorer et mettre sous le boisseau le savoir lumineux de la science grecque légué par Ptolémée.
Hipparque (-190 / -120)
Les travaux d’Hipparque, qui va constituer le principal référent de Ptolémée, dans la seconde moitié du 2e siècle avant notre ère, sont parmi les plus riches de l’astronomie antique. Hipparque a notamment découvert le phénomène de précession – le lent décalage de la position des étoiles sur la voûte céleste – et dressé la première carte précise du ciel, recensant entre 800 et 1 600 étoiles. De nombreux astronomes postérieurs se sont référés à ce catalogue, qui a disparu. De tous les écrits d’Hipparque, seuls ses Commentaires, qui discutent la description du ciel d’Eudoxe et d’Aratos, nous sont parvenus.
Un astronome de l’Université de Louisiane, Bradley Schaefer, c’est l’auteur de l’article auquel j’ai fait allusion, pense avoir retrouvé sur l’Atlas Farnèse, un marbre de plus de deux mètres de hauteur qui représente le titan Atlas portant un globe céleste sur ses épaules, une figuration du catalogue d’Hipparque. Cette sculpture, conservée à Naples, est une copie romaine du 2e siècle d’un original grec.
Voici une reproduction de cet Atlas – ainsi qu'une reproduction (à toutes fins utiles) sans feuille de vigne :

cliché : Griffith Observatory, source : http://www.expeditionzone.com

Sur le globe, d’un diamètre de 65 centimètres, 41 figures représentant les constellations sont sculptées avec les cercles armillaires, l'équateur, l'écliptique, les tropiques, les cercles arctique et antarctique et les colures (deux cercles de référence perpendiculaires à l'équateur). En raison du lent déplacement du point vernal (du latin : ver, veris : printemps, soit le point où se trouve le Soleil le jour de l'équinoxe de printemps, dans l'hémisphère nord) sur le zodiaque, la position du soleil décrit un cercle et retrouve sa position initiale tous les 26 000 ans. Pour les Sumériens, l’équinoxe de printemps se produisait dans la constellation du Taureau (supra : chapitre 2.10). Le point vernal rétrograde de 50” 26’ par an (en tenant compte de la force exercée par les autres planètes sur la Terre, agissant dans le sens opposé) et change de constellation tous les 2 140 ans. Il se situe actuellement dans la constellation des Poissons et progresse en direction du Verseau (qu’il atteindra dans six siècles environ). C’est précisément le phénomène de précession qui permet à Schaefer d’attribuer à Hipparque la position des constellations du globe porté par Atlas – qui correspondrait au ciel de la fin du 2e siècle avant notre ère.
Ératosthène (-276 / -194)
Le nom d’Eratosthène est associé à la mesure de la circonférence de la terre, dans un raisonnement qui met en œuvre les ressources de la géométrie, de la trigonométrie et de l’expérience. Ce sont les attendus ou les pré-requis de ce raisonnement que je souhaite présenter brièvement ici, rappelant que l’évidence (ou ce qui nous semble tel) requiert un travail de l’esprit (qui se solidifie parfois en évidence, en effet, cela s’appelle la transmission culturelle), produit de la réflexion et de l’imagination créatrice de plusieurs générations de savants. Il en va ainsi de l’astronomie grecque. Ératosthène que je prends pour point de départ étant, bien entendu lui-même, un héritier. Peut-être avez-vous lu le roman de Denis Guedj : Les cheveux de Bérénice (Bérénice est la constellation qui se trouve entre la Vierge, le Lion, la Grande Ourse et Arcturus) qui met en scène la réalisation de cette mesure. Le calcul que je vais présenter est fort simple (c’est un exercice qu’on fait aujourd’hui en classe de Seconde – et qu’on faisait autrefois en classe de Quatrième, il me semble) et on peut considérer, à lire les Cheveux de Bérénice, qu’il y a du paradoxe à étendre sur 375 pages ce qui se comprend dans l’instant. Mais la connaissance de l’environnement culturel de l’Égypte ptoléméenne est utile, précisément, pour caractériser la représentation du monde et le savoir qui soutiennent ce calcul.
Ératosthène était directeur de la fameuse bibliothèque d’Alexandrie, fondée au 3e siècle avant l’ère chrétienne par Ptolémée Sôter et Démétrios de Phalère (disciple d’Aristote, chef du parti favorable aux Macédoniens, élu, grâce à leur appui, archonte décennal en 317, il se réfugie en Egypte en 307 quand Démétrios Poliorcète s’empare d’Athènes). La Bibliothèque était le centre culturel de toute la Méditerranée. On y trouvait les écrits de Sophocle, Euripide, Homère, Hippocrate, l’œuvre d’Aristote (-384 / -322) et les œuvres des savants les plus réputés. Callimaque, le prédécesseur d’ Ératosthène, réalise un catalogue qui archive et ordonne tous les documents présents. La bibliothèque aurait ainsi possédé plus de 500 000 rouleaux.
Les conditions épistémologiques de ce raisonnement sont (principalement) les suivantes.
Il suppose en effet :
- Que la terre est une sphère ;
- Que l’analyse mathématique peut être appliquée aux corps célestes (que les rayons du soleil, par exemple, peuvent être assimilés à des droites parallèles) ;
- Il se soutient, aussi, du travail de modélisation dans la description du monde. Un des principaux apports de Ptolémée à la mesure du monde va consister dans ce recours systématique à la modélisation et au calcul.
La terre est une sphère.
L’idée que la terre est une sphère est un des principaux héritages de l’âge grec. Militent en faveur de cette idée un argument esthétique (pour les pythagoriciens et les platoniciens, la sphère est la forme mathématique la plus parfaite) et des arguments d’observation :
“Qui plus est dit Aristote : la sphéricité de la terre nous est prouvée par le témoignage de nos sens […] alors que dans les phases mensuelles de la lune, les segments sont de toutes espèces […] dans les éclipses, la démarcation est toujours arrondie. Cette ligne courbe, si l’éclipse est due à l’interposition de la Terre, signifie donc la sphéricité de celle-ci.” (Traité du ciel, II ; 14)
et Strabon : “C’est la courbure de la mer qui intercepte la vue des navigateurs et les empêche d’atteindre du regard les lumières lointaines situées à hauteur de leurs yeux.” (Géographie, I, 1, 20) Les arguments de Cléomède ou de Marin de Tyr sont du même ordre.
En réalité, je l’ai rappelé, la géométrie des Grecs paraît indissociable de l’astronomie. Le traité d’Autolycos de Pitanè, intitulé La sphère en mouvement et daté des années - 330, traite d’un même esprit de géométrie et d’astronomie.
Les observations d'Eratosthène
En 205, Eratosthène conçoit et met en œuvre une expérience pour mesurer la longueur du méridien terrestre (circonférence passant par les pôles) à partir de deux points : Syène (avant la première cataracte du Nil, aujourd'hui Assouan, célèbre pour son barrage) et Alexandrie. Pour Eratosthène, comme pour tous les Grecs, au moins depuis Anaximandre au 6e siècle, la terre est une sphère. La géométrie peut donc s’y appliquer. Dans les Phénomènes d’Euclide (c. 300 avant notre ère), la géométrie est explicitement appliquée à la sphère céleste. Pour les Grecs, également, la terre est un point par rapport à la sphère céleste en mouvement. C’est aussi un argument présent dans les Phénomènes, argument que Ptolémée fera sien : quel que soit le point d’observation sur terre, l’observateur se trouve toujours au centre de la sphère céleste.
Vous connaissez la formule d’Hérodote : “L’Égypte est un don du Nil”. La mesure de la terre est aussi un “don du Nil”. Il se trouve en effet que le cours du Nil vers la mer suit, à quelque chose près, le méridien terrestre (Syène est à 24°5’de latitude Nord et Alexandrie à 31°12’, cette différence n'affectant pas sensiblement le calcul). “Le méridien de Syène, écrit Strabon (Géographie, II, 5, 7) décrit à très peu près le cours du Nil, approximativement de Méroé à Alexandrie, soit sur quelque dix mille stades.” Cette donnée permet la synchronisation de la mesure de l'ombre à Alexandrie (midi vrai) quand il est midi à Syène.

Syène (aujourd'hui Assouan)
Halte de l’Armée Française à Syène en Haute-Egypte.
Huile sur toile 112 x 164 cm par Jean- Charles Tardieu.
Château de Versailles
Eratosthène pose qu’il en est bien ainsi. L’argument mathématique qu’il va utiliser, contenu dans les Éléments d’Euclide, est le suivant : “Deux droites parallèles coupées par une sécante forment des angles alternes internes égaux”. L’hypothèse cosmologique rappelée précédemment, savoir que la terre est un point dans la sphère céleste, permet d’affirmer que les rayons du soleil, provenant d’une source très éloignée de la surface du globe (150 millions de kilomètres, en réalité), sont parallèles. Si les rayons du soleil sont parallèles, alors les angles formés par les ombres portées peuvent être assimilés à ceux formés par une sécante qui coupe deux droites parallèles. Ce raisonnement commande l’expérience qui suit.
La ville de Syène se situe à peu près sur le tropique du Cancer. De ce fait, à midi au moment du solstice d’été, le soleil culmine dans le ciel. Le soleil, se trouvant à la verticale, éclaire le fond d’un puits (et les ombres portées des objets verticaux sont parfaitement centrées). Au même moment, à Alexandrie, 5000 stades plus au nord (environ à 800 kilomètres de Syène - 787 km), sur le même méridien, on mesure l’ombre, courte et décentrée, d’un obélisque dont la hauteur est connue. Cette mesure permet de calculer l’angle que font les rayons du soleil avec la verticale soit :
â = 7,2° (ou 7,12)
Il suffit maintenant, si la Terre est sphérique, de prolonger la verticale d'Alexandrie (l'obélisque) et celle de Syène (le puits). Ces deux verticales vont se rejoindre par définition au centre de la Terre. Les rayons solaires étant parallèles, l'angle formé par les deux verticales au centre de la Terre est donc égal à celui formé par l'ombre de l'obélisque, soit 7,2°.
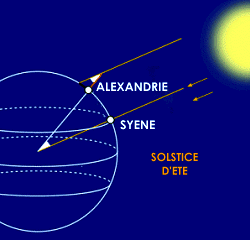
La valeur de cet angle dont l’arc est connu (c’est la distance séparant les deux villes) rapporté à la circonférence du cercle permet de calculer la circonférence de la terre sans autre forme de procès. 360° divisé par 7,2° donne 50. Ératosthène aurait ainsi estimé la circonférence terrestre à 250 000 stades soit, pour une valeur du stade de 157,50 mètres, 39 600 kilomètres, valeur proche des 40 000,07 kilomètres réels.
Ce calcul démontre la puissance de l’astronomie et de la trigonométrie, dont Ptolémée va systématiser l’emploi, pour arpenter le monde. L’expérience d’Ératosthène a vraisemblablement bénéficié de l’appui de l’administration ptoléméenne (lagide) pour calculer la distance entre Syène et Alexandrie. Les intendants royaux avaient en effet à leur disposition des opérateurs et des outils appropriés à ce calcul. Ces fonctionnaires employaient des “compteurs de pas” (bématistes), spécialistes chargés, depuis Alexandre, de fournir aux armées les informations sur les itinéraires, des experts pour tenir le cadastre et calculer la surface (variable en fonction des crues) des champs cultivés – et usaient de “nilomètres”, puits creusés sur les rives du Nil, gradués sur leurs parois, qui permettaient de déterminer l’assiette de l’impôt, les récoltes étant fonction de l’importance de la crue du Nil.

Puits-nilomètre de Kôm Ombo, à environ 40 kilomètres au nord de Syène
(temple de l’époque ptolémaïque, dit “aux deux divinités” ,
Haroëris, le dieu à tête de faucon et Sobek, le dieu crocodile : on peut y voir des momies de cet animal ;
le temple, bâti sur une colline, domine une boucle du Nil et le site commandait vraisemblablement l’accès à l’or de la Nubie - Noubet : “or”)
Mais ce que cette expérience vient de démontrer – et comment ! puisque le monde connu, l’œkoumène, est borné – c’est qu’il n’est pas nécessaire d’avoir parcouru le globe pour en faire le tour. La mesure de la terre peut s’affranchir du pas de l’homme. Il suffisait d’y penser ! Bien sûr. Il y a dans cette formule à la fois quelque chose de juste et quelque chose d’injuste. S’il suffisait d’y penser, pourquoi personne n’y a-t-il donc pensé avant Ératosthène ? Mais c’est dire aussi que cette opération, que tout un chacun peut refaire (et qui constitue un exercice pédagogique banal) était déjà là, préparée par l’empilement du savoir opéré par les générations précédentes. C’est le grand Newton qui disait : “Nous sommes des nains juchés sur les épaules de géants” (jugement de Bernard de Chartres qui peut s'interpréter de différentes manières ; ainsi : "Nous voyons plus loin qu'eux"…; l'original énonce : " Nous les théologiens d'ici, sommes des nains juchés sur les épaules de géants, grâce à eux notre vue porte plus loin ".)
J’ai rapporté ici l’expérience telle qu’on la trouve exposée dans les manuels (et sur le Net où j’ai effectué quelques “copier-coller”). Des auteurs, comme l’astronome Jean-Baptiste Joseph Delambre (celui qui a “mesuré” le Mètre : soit le dix millionième du quart du méridien terrestre), dans son Histoire de l'astronomie, 1817-1827, se sont interrogés sur l’expérience d’Ératosthène qui nous est connue grâce aux relations – postérieures – de Cléomède (contemporain de Posidonius) et de Strabon (c. -64 / +23). La difficulté de la mesure de l’angle du gnomon (Delambre conteste, par exemple, la pertinence de l’utilisation d’un scaphé – cadran solaire constitué d’une aiguille verticale qui fait une ombre sur une surface hémisphérique concave – attestée par Cléomède – pour un tel calcul), l’approximation de l’estimation de la distance entre Syène et Alexandrie, le biais du diamètre apparent du soleil (l’angle sous lequel on voit cet astre depuis la terre)… lui paraissent constituer des conditions expérimentales rédhibitoires. Une compensation d’erreurs a probablement permis l’obtention du résultat cité… Cette suspicion n’affecte évidemment pas la valeur du raisonnement. “Tout était donc incertain dans son calcul, écrit Delambre (op. cit. p. 89), mais ce calcul était d’un homme d’esprit qui aperçoit ce qu’il faudra faire pour obtenir avec précision la grandeur de la Terre, quand on aura des données plus exactes.”
L’autre méthode, proposée par Poséidonios (Posidonius d’Apamée, c. -135 / -51)
Canope était une ville voisine d’Alexandrie (célèbre dans l’antiquité pour la dissolution qui était supposée y régner), mais aussi l’étoile la plus brillante du ciel austral, que les marins utilisaient pour se guider de la Grèce à l'Égypte. Canope apparaît au niveau de l’horizon à Rhodes et culmine à 7,5 ° à l’horizon d’Alexandrie, deux villes que l’on situait sur le même méridien. L’arc terrestre séparant Rhodes et Alexandrie vaut donc les 7,5 ° qui marquent la différence de hauteur de Canope au-dessus de l’horizon dans ces deux villes. La méthode est géométriquement juste, mais génératrice d’erreurs… que Ptolémée fera siennes. Le raisonnement de Posidonius montre, quoi qu’il en soit, que le recours au calcul des angles était “banal” pour les Grecs. C’est dans un même esprit qu’Hipparque, en mesurant la durée d’une éclipse de lune, avait estimé que celle-ci se trouve à 65 rayons terrestres du centre de la Terre (ce qui est proche des 60,25 rayons terrestre réels) et que le rayon de la lune était égal au tiers du rayon terrestre (0,25).
*
Claude Ptolémée (100-180)
"La géographie partage la Terre selon les cercles du Ciel"

Ptolémée, dans la fresque de Raphaël au Vatican L'Ecole d'Athènes
Ptolémée est représenté de dos, portant la couronne. Strabon lui fait face, tenant la sphère étoilée.
(La Renaissance considère Strabon comme celui qui a mis en correspondance l’astronomie et la cartographie, Géographie : II, 5, 4)
Claude Ptolémée vécut au 2e siècle de notre ère à Alexandrie. Les titres de ses différents ouvrages : Almageste (c’est le nom que les Arabes donneront à sa Syntaxe mathématique : le Grand traité), Tetrabiblos (qui traite d'astrologie), Géographie, Harmonica, Optique, ... attestent de son intérêt pour l’ensemble des disciplines scientifiques de son temps. Dans les différents domaines où il a œuvré, Ptolémée semble s’être attaché à réaliser des synthèses du savoir, et à les vulgariser dirait-on aujourd’hui. L’originalité de ses travaux a parfois été mise en doute. On l’a notamment suspecté d’avoir repris le catalogue d’étoiles réalisé par Hipparque et, comme on sait peu de choses de lui, on a pu en faire un auteur fictif, une manière de Bourbaki dont les travaux auraient eu pour objet de rassembler en divers traités le savoir du temps.

Attribué à André Thevet (1502-1590), Claude Ptolomée Pelusien,
gravure au burin, couleur ajoutée à l’original, 17,1 x 14,3 cm, New York, Collection Granger, 234.09
De fait, le premier ouvrage de Ptolémée, la Syntaxe mathématique, consiste en une mise en ordre (syn-taxis), une synthèse ordonnée des connaissances sur le système du monde, telle que l’astronomie et la géographie mathématique peuvent nous le représenter. Ptolémée est vraisemblablement, avec Strabon, le “père” de la géographie (Ératosthène ayant été le premier auteur à user de ce terme pour intituler l’un de ses ouvrages). Je résumerai cette paternité dans une opposition dont je vais donner le contexte : tandis que la chorographie (khora : contrée, la description, la topographie) rapporte ce qui se voit à l’œil, la géographie décrit ce qui se voit par l’esprit. La géographie ne s’épuise pas dans la seule observation, elle n’a pas pour objet l’empirie, c’est une science et c’est le calcul qui lui donne ses outils. “La géographie, développe Ptolémée, est une imitation graphique de la partie connue de la terre […] dans son unité et sa continuité […] Tandis que la chorographie a pour objectif l’étude des réalités partielles […] la géographie, elle, vise à donner une vue d’ensemble.” (Géographie, I, 1) “L’étude de la forme et des dimensions de la terre entière, la connaissance de sa position par rapport au ciel sont des préalables indispensables si l’on veut être capable d’indiquer les dimensions et les caractéristiques de la partie connue de la terre, d’indiquer aussi les parallèles de la sphère céleste sous lesquels se trouvent chacun des lieux du monde connu.” (les italiques sont nôtres) (I, 6) Ce dernier membre de phrase indique une manière de subordination des localisations terrestres par rapport au système de coordonnées, à la construction mentale qui permet de les situer, de les faire exister géographiquement, en quelque sorte.

Juste de Gand (Joos van Gent) et Pedro Berruguete, CL PTOLEMAEO [AL]EX, vers 1476, peinture à l'huile sur bois, 98 x 66,3 cm,
Paris, Musée du Louvre, acquis en 1861, n° MI 657.
Le propre du géographe, c’est en effet de prendre de la hauteur. Strabon écrit (Géographie, II, 5, 1) : “Le simple fait de tracer sur une même surface plane l’Ibérie, l’Inde et tous les pays intermédiaires, tout autant que de déterminer couchants, levants, passages au méridien, comme s’ils étaient les mêmes pour tous exige une réflexion préalable sur la disposition et le mouvement du ciel, une claire conscience que la surface de la terre, sphérique dans la réalité, n’est actuellement représentée en plan que pour les besoins de l’œil ; la formation reçue est alors proprement géographique ; dans le cas contraire, pas de géographie possible [...] Aussi bien le géographe ne destine-t-il pas sa géographie à l’homme du pays, ni au citoyen éclairé qui n’a jamais eu souci de ce qu’on nomme proprement les mathématiques, pas davantage au moissonneur et au laboureur, mais seulement à qui peut admettre que la terre dans son entier a la forme que lui attribuent les hommes de science, avec les conséquences qu’entraîne un tel préalable.” Cette subordination de la représentation du monde à cette “science première qu’est la physique” (II, 5, 2), à rebours des imaginations de la doxa populaire, confère au géographe, si je puis dire, comme on le voit sur la représentation du globe de l’Atlas Farnèse (supra) où les constellations sont portées sur la surface du globe, le point de vue de Sirius. C’est la projection des cercles célestes sur la Terre qui fonde la géographie. “De même que le géomètre, pour mesurer la terre, a pris ses prémisses chez l’astronome, que l’astronome a emprunté au physicien, de la même manière le géographe doit emprunter au géomètre qui a mesuré le globe terrestre pour, de là, prendre son élan, se fiant à lui et à ceux à qui celui-ci s’est fié.” (II, 5, 4) “Sous chacun des cercles célestes se projette son homonyme terrestre, et il en est de même pour les zones” (II,5,3). Bien sûr, Ptolémée n’a pas inventé le GPS (!) (qui utilise la triangulation – décrite par Thalès), mais il met, lui aussi, le cartographe en position d’observateur absolu. Substituant aux réseaux orthogonaux de Marin de Tyr, un système de projection de la sphère sur le plan (conique simple, Géographie : I, 24, 1 et conique homéotère, I, 24, 9), Ptolémée fonde la cartographie moderne et permet la représentation des grands espaces. Ce changement d’échelle, qui met le globe à portée, ouvre le monde.
Un trait marquant de la méthode ptoléméenne, c’est en effet le primat de la trigonométrie sur l’estimation (quand bien même sa Géographie y fasse parfois exception). Car l’évaluatation des distances en stades, constate Ptolémée, se fait à l’aide d’“images”, au jugé. “La méthode astronomique [elle] n’a nul besoin d’une évaluation en stades pour établir le rapport entre les diverses parties de la terre, ni pour dresser le plan d’ensemble de la carte, car il suffit de supposer à la circonférence terrestre un nombre donné de segments.” Ce qui importe donc, c’est la mesure des arcs en degrés (qu’il appelle ici segments) et non la mesure des distances terrestres en stades… Je rappellerai ici que la trigonométrie, “l’art de trouver les parties inconnues d’un triangle par le moyen de celles qu’on connaît” dit d’Alembert dans l’Encyclopédie (1751), n’est pas initialement un outil de calcul du triangle, mais du cercle. C’est une géométrie appliquée à l’étude du ciel. Elle est indissociable de l’astronomie. On attribue à Hipparque les premières tables trigonométriques, qui font correspondre la valeur de l’angle au centre et la longueur de la corde interceptée dans le cercle. La corde d’un angle  est égale à 2sin(Â/2). (Le calcul du sinus, du sanscrit jina : corde, est dû à l’astronomie indienne ; il prend en compte la demi-corde de l’angle double plutôt que la corde de l’angle.)

Anonyme, Ptolémée, dans la Cosmographie, 1472, Rome, Biblioteca Apostolica Vaticana (Codes Urb. lat. 277, fol. 3r.)
L’hypothèse géocentrique
Bien sûr, le nom de Ptolémée reste associé pour nous au géocentrisme, à une représentation du monde obsolète… L’hypothèse héliocentrique n’est pourtant pas inconnue de la science grecque. Elle est avancée vers 280 avant notre ère par Aristarque de Samos. L’hypothèse géocentrique suppose la rotation de la sphère des fixes autour de l’axe des pôles et explique le mouvement irrégulier des planètes, littéralement : (astres) errants, par des images illustrant la relativité du mouvement. Ainsi, rapporte Cléomène, “on pourrait se représenter les étoiles fixes comme des passagers qui, sur un navire, restent chacun à la même place, et les planètes comme des passagers qui se déplacent en sens contraire du bateau, allant de la proue à la poupe en un mouvement assez lent…” (I, 3)
Un apport de la pensée grecque tient dans son génie de la modélisation ; on vient d’en voir un résultat avec Ératosthène. Dans l’hypothèse géocentrique, le “ciel des fixes” est assimilé à une sphère, animée d’une rotation uniforme sur son axe. Au centre se trouve la terre, immobile et réduite à un point. D’après Diogène Laerce, à Millet au 6e siècle, Anaximandre avait “construit la sphère” et Eudoxe de Cnide, deux siècles plus tard, y ayant porté les constellations, en expliquait le fonctionnement dans un traité intitulé Les phénomènes. Cet ouvrage, traduit en vers par Aratos, fait l’objet du Commentaire d’Hipparque. À la suite des astronomes babyloniens, Hipparque divise le cercle en 360° et établit les premières “tables de cordes”. C’est grâce à ces tables qu’il découvre que l’axe de la terre n'est pas fixe, en comparant ses observations à celles de l’astronome alexandrin, Timocharis, effectuées 150 ans plus tôt. Ptolémée explique comment calculer des longueurs de cordes et en publie un catalogue.
La Géographie (Cosmographia) comporte huit livres. Les deux premiers donnent les principes généraux de l’établissement des cartes du monde connu. Ptolémée y expose les différents types de projections. Il discute les travaux cartographiques et les évaluations de Marin de Tyr (IIème siècle) qui constituent néanmoins, vraisemblablement, sa source principale. Du livre II au livre VII, il donne des listes de longitudes et de latitudes, en degrés, de 8 000 localités, classées par continent et région, et la liste de 300 villes, identifiées par leurs coordonnées, la durée du jour le plus long dans chacune d’elle ainsi que les heures mesurées depuis le méridien d'Alexandrie. Eratosthène avait divisé la sphère terrestre en soixante parties, Hipparque conçu une cartographie fondée sur la détermination astronomique des latitudes et des longitudes et, je l’ai dit, divisé la surface de la sphère terrestre en 360 parties (qui ont donné les “degrés” de la géographie moderne, subdivisés en minutes et en secondes d’arc) ; c’est ce système que Ptolémée va mettre en œuvre et perfectionner. Il parachève le savoir technique de confection des cartes (il est probablement le premier à utiliser la projection conique homéotère) et y porte les dernières connaissances géographiques. Dans sa conception générale et dans son vocabulaire, la cartographie d’aujourd’hui hérite de cet achèvement. Ainsi les termes de “latitude” et de “longitude” (la partie connue de la terre étant plus large de l’ouest à l’est que du nord au sud, elle est appelée “longueur”, ou longitude, par rapport à la “largeur”, ou latitude, qui désigne la distance angulaire d’un point par rapport à l’équateur) la notion d’antipodes, l’usage d’orienter les cartes le nord en haut et l’est à droite, la conception d’outils et de modèles et leur mode de fabrication, la généralisation de la notion d’échelle, la mise au point de méthodes de projection des surfaces sphériques…

Parisanus graecus 1401, fol. 2. Bibliothèque Nationale.
Armé de ces outils, il est possible de représenter le monde habité et de pressentir le monde à découvrir. En mathématiques, l’esprit fait tour de la sphère sans rencontrer d’obstacle.
La géographie ptoléméenne relève, en réalité, d’une cosmographie mathématique qui englobe dans un tout (harmonieux, comme le mot cosmos l’indique) le système céleste, la terre et – Ptolémée est également théoricien de l’astrologie, dans le Tetrabiblos – les hommes. C’est en ce sens qu’elle se sépare, stricto sensu, du savoir scientifique tel que nous l’entendons. Plus prosaïquement, ayant sondé par les astres les “calculs des dieux” concernant les destinées humaines, Ptolémée fait entrer les calculs des hommes – l’expansion de l’Empire – sur la carte du monde, dans les “cercles du ciel”. La guerre, ça sert aussi à faire avancer la géographie... de même que la géographie la colonisation : “Il est clair, écrit Strabon, que la géographie tout entière est orientée vers la pratique du gouvernement.... Il serait plus facile de prendre en mains un pays si l'on connaissait ses dimensions, sa situation relative, les particularités originales de son climat et de sa nature" (I,1,16). L’empereur Auguste avait chargé Marcus Vipsanius Agrippa (64 - 12) d’établir une carte monumentale de l’Empire. Cette carte était placée sur le Porticus Vipsaniæ, le long de la Via Flaminia, à proximité de l’autel de la Paix. Le siècle de Ptolémée est ainsi un siècle de mise en valeur et de consolidation des limites du Dominium. Les Antonins, Trajan (qui règne de 98 à 117), Hadrien (de 117 à 138), Antonin (de 138 à 161) et Marc-Aurèle (de 161 à 180) voyagent et s’emploient à développer les échanges entre les provinces. Hadrien, par exemple, visite Alexandrie et remonte le cours du Nil. L’extension du monde romain est liée à la fois aux expéditions militaires et à la création de nouvelles routes commerciales. Les relations avec l’Inde, ouvertes par l’expédition d’Alexandre, se développent par terre et par mer (depuis qu’Hippalos a mis en évidence le régime des moussons), pour le commerce des épices. Avec la Chine, pour le commerce de la soie. Marin de Tyr, cité par Ptolémée, a recueilli le témoignage d’un commerçant macédonien nommé Maes Titianos ayant envoyé des agents chez les Sères (les Chinois), dans les années 120, qui ont rapporté des informations sur les chaînes du Pamir, du Tian Chan, de l’Altaï et sur les montagnes de la Chine... Vers le sud, aux confins de l’Afrique, les expéditions de Cornelius Barbus (sous le règne de Tibère, vers l’an 20) et de Septimius Flaccus (sous Vespasien), qui ont à la fois pour but le contrôle de populations en rébellion (notamment des Garamantes, peut-être issus des “peuples de la mer”) et le commerce (de l’ivoire ou de fauves), permettent d’atteindre le mystérieux pays d’Agisymba, où “prospèrent la race des éléphants et les animaux insolites”. (I, 9, 7) A propos des sources du Nil, dont les crues régulières étaient un sujet d’étonnement pour les Anciens, Ptolémée développe une explication en se fondant notamment sur le récit, utilisé par Marin de Tyr, d’un marin dénommé Diogène, déporté par le vent de mousson vers le sud jusqu’au cap Rhapta (Dar es Salaam ?). Il apporte des informations, coordonnées à l’appui, sur des montagnes d’Afrique situées au-delà des itinéraires connus, au sud des lacs du Nil : “les Monts de la Lune” (IV, 9, 6) qui se trouvent à l’extrémité sud-est de la partie connue de l’Afrique et dont les neiges, en fondant, alimentent les lacs situés plus au nord, d’où sortent deux cours d’eau dont la réunion forme le Nil. (IV, 8, 3)
De fait, comme le note encore Strabon, “ les Romains et les Parthes, en étendant leur empire, ont beaucoup ajouté à notre connaissance de la géographie, de même que jadis l’expédition d’Alexandre, comme le soulignait Ératosthène. Alexandre nous a découvert la majeure partie de l’Asie et tout le Nord de l’Europe jusqu’à l’Istros (le Danube) ; les Romains, tout l’Ouest de l’Europe jusqu’à l’Elbe qui divise en deux la Germanie, ainsi que les pays situés plus loin que l’Istros jusqu’au Tyras (le Dniestr) ; les régions situées encore au-delà, jusqu’aux Méotes (population de la mer d’Azov ?) et au littoral qui finit en Colchide, nous ont été révélées par Mithridate surnommé Eupator, ainsi que par ses lieutenants ; les Parthes à leur tour nous ont familiarisés avec l’Hyrcanie, la Bactriane et les pays voisins, ainsi qu’avec les peuples scythes qui leur font suite, beaucoup moins connus précédemment. Aussi avons-nous des chances de pouvoir en dire plus long que nos prédécesseurs" (I,2,1). Et c'est le monde “heureusement habité", c'est-à-dire, non seulement là où l'homme peut vivre, mais riche en ressources qui intéresse un Strabon, formant le dessein d'instruire “l'homme désireux de savoir et tourné vers l'action” (I, 1, 23) mais aussi d'être utile à l'administration et au gouvernement de l'imperium romanum.
Avec l’état du savoir de la science grecque, la description des terres connues et les outils pour appréhender les terres à découvrir, Ptolémée lègue une représentation rationnelle du monde. Rationnelle, c’est-à-dire accessible à la mesure de l’homme avec ce réseau des latitudes et des longitudes permettant de quadriller le globe. Il suffirait aux continuateurs de porter les connaissances nouvelles sur cette sphère dont l’esprit a déjà fait le tour. L’aventure de l’exploration de la planète commence par cette projection idéale fondée sur la vérité mathématique de la trigonométrie. Une telle mimésis, cette “imitation graphique de la terre […] dans son unité et sa continuité” autorise et appelle la circumnavigation. Si Colomb n’avait pas cru en la rotondité de la terre, il ne serait évidemment pas lancé dans l’aventure vers l’Ouest.
Puisque j’ai annoncé un parallèle entre Ératosthène et Ptolémée, je rappellerai en manière de conclusion de cette rapide présentation que, touchant la circonférence du globe, c’est Eratosthène qui est dans le vrai, mais que c’est grâce à l’erreur de Ptolémée que Christophe Colomb a découvert l’Amérique. Ptolémée, en effet, confiant dans la supériorité du calcul des angles et des cordes sur la mesure, suit Strabon qui, rapportant les résultats d’Ératosthène et de Posidonius, décrète sans autre forme de procès que la circonférence de la terre est de 180 000 stades et qu’il est possible de toucher l’Inde en moins de 70 000 stades. Ptolémée donne à chaque degré une valeur équivalente à 80 kilomètres, au lieu de 112, ce qui confère à la circonférence du globe la valeur de 28 000 kilomètres. Propagandiste du calcul et préférant, paradoxalement, la vraisemblance à la mesure, il étire démesurément l’Asie vers l’est : sur 180° au lieu de 130° environ. Oui, pour découvrir le Nouveau Monde, il fallait croire à la rotondité de la terre, mais il n’était pas mauvais, non plus, d’estimer la distance à parcourir bien moindre… Sur le globe de Martin Behaim, réalisé à Nuremberg en 1492, l’Europe, étendue sur 230°, fait directement face au Japon. Pour emporter la décision de ses commanditaires, Colomb aurait d'ailleurs utilisé, de surcroît à son argumentation cosmographique, l’Imago Mundi du Cardinal Pierre d’Ailly (1350-1420) qui argumente, sur la foi des Evangiles Apocryphes, que, les eaux ne représentant qu’un septième de la surface émergée, l’Asie et l’Europe sont proches.

Globe de Martin Behaim, http://gallery.sjsu.edu/cartography
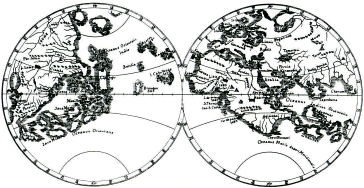
Planisphère de Martin Behaim, 1492
Le Japon est situé à la longitude des îles Caraïbes :
Quoi qu’il en soit de cette erreur, l’exploration de la planète peut se poursuivre.
Le “ fénoir” théologique : la géographie de l’imaginaire
Pendant plus de dix siècles, pourtant, le génie humain illustré par la science grecque va se trouver recouvert par une vision théologique du monde. Le terme même de géographie disparaît (pour désigner la Géographie de Ptolémée, les auteurs de la Renaissance utiliseront le terme de “cosmographie”). La géographie, comme telle, n’avait sa place ni dans le “quadrivium” ni dans le “trivium”, les arts libéraux du Moyen Age.
Le Vatican n’a pas seulement mis une feuille de vigne sur les statues de la mythologie, il en a mis aussi sur le savoir. Le fait est connu : c’est la science indienne et arabe

Almageste
Ptolemae magnae constructionis, Libri XIII
Parchemin, IXe siècle.
(Paris, BnF, Dép. des Manuscrits, Grec 2389, fol 54)
et sa traduction en arabe :

qui transmettront et vivifieront l’astronomie des anciens Grecs. Sur cette amnésie scientifique se construit une géographie de l’imaginaire qui révèle sans doute les formes archétypales de la psyché humaine mais dont la valeur descriptive, à l’inverse de ce qu’elle fait accroire, est nulle.
Nous disposons ainsi de plus de six cents mappemondes produites par ces géographes poètes du Moyen Âge. Ces cartes “théologiques” ont généralement pour centre Jérusalem. Le monde habité, explique par exemple Isidore de Séville au 7e siècle (qui admet, par ailleurs, l’idée de la rotondité de la terre, mais telle qu’on la représente sur les fameuses cartes T en O, où “T” représente la Méditerranée entre les trois continents et “O” le fleuve océanique entourant le monde)

Carte "T en O".
Gossuin de Metz, L'Image du monde. Copie du XIIIe siècle. Manuscrit sur parchemin (6 x 6 cm)
BnF, Manuscrits (Fr 1607 fol. 43)
a été partagé entre les trois fils de Noé, Sem, Cham et Japhet et la carte du monde est le résultat de ce partage, parfois figuré sur trois feuilles, comme trois feuilles de trèfle. Cette tripartition physique dit assez le caractère idéal de cette représentation où c’est le mythe (et non la projection des cercles célestes) qui tient la main du cartographe. Bien entendu, la terre est redevenue plate et les Solin (3e siècle), Orose (5e siècle), Cosmas d’Alexandrie (6e siècle – Cosmas doit son nom teknonyme à ses talents cosmographiques), font la description, aussi minutieuse qu’invraisemblable, de ses merveilles.
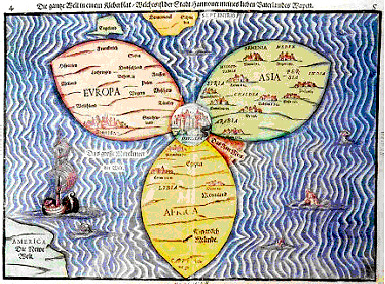
L'œkoumène chrétien est donc plat, le plus souvent circulaire et divisé en trois parties par l'inscription de la lettre T dans le cercle. Dans la mappemonde de Zacharia Lilio (Orbis Breviarum, Florence 1493), le montant du T figure la Méditerranée qui sépare l'Europe et l'Afrique et les deux moitiés de la traverse du T le Nil et le Tanais (le Don). Au XIIe siècle, Pierre Comestor, auteur d'une Historica Scolastica, peut écrire de Jérusalemen : “Certains disent que cet endroit est le nombril de la terre habitable, parce que tous les ans, un certain jour d'été, à l'heure de midi, le soleil descend jusqu'à l'eau du fond d'un puits, sans faire aucune ombre nulle part, phénomène que les philosophes disent avoir lieu à Syène.” Exemple achevé de dégradation de l'héritage scientifique, de dissipation du patrimoine, dans le mythe.
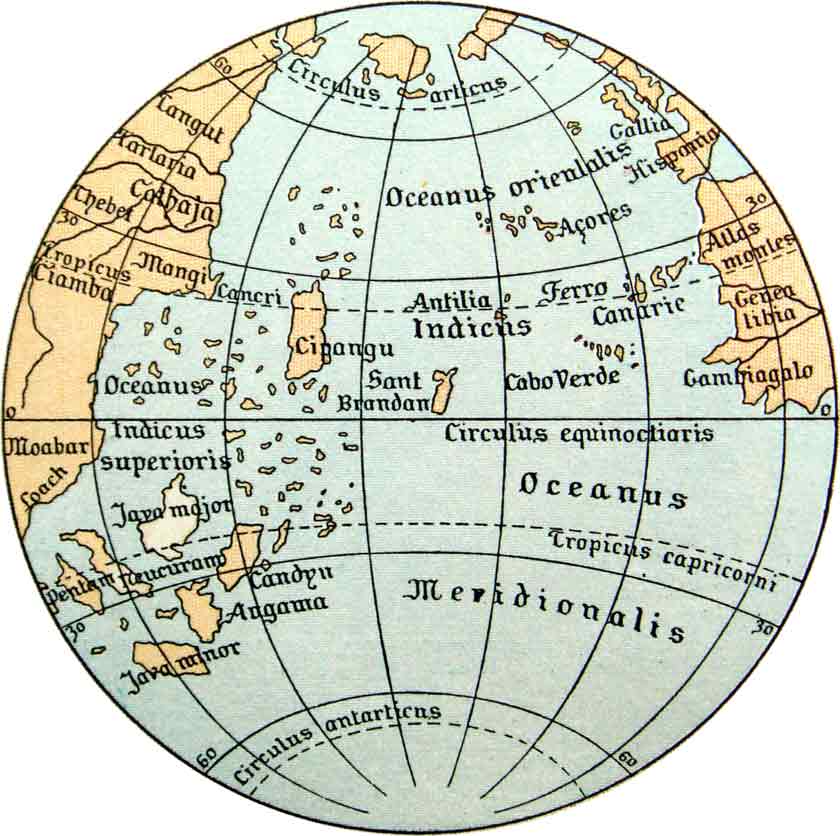
Comparant la carte d’Eratosthène (ou celle, plus récente, de Posidonius, infra) avec la carte du monde de Ptolémée (pour une comparaison des cartes antiques, cf. Louis Figuier, La Terre et les Mers, ou description physique du globe, Paris, Librairie Hachette, 1884), on voit désormais un monde qui paraît ouvert à l’exploration. Ptolémée discrédite définitivement l’idée homérique d’une pangée confinée, contenue par un océan inauspicieux. L’œkoumène cesse d’être représenté comme une île (en forme de chlamyde, disait-on : Strabon, II, 5, 6) avec Rhodes (où passe, depuis Eratosthène, l’un des deux axes de référence du monde habité - Strabon, II, 5, 7) pour centre. Il représente le continent austral en prolongement de l’Afrique et, dans sa Géographie (I, 10, 1), porte les terres jusqu’à 16° de latitude. Cette mention d’une “terre inconnue”, “au midi”, “fermant la mer de l’Inde” (VII, 5, 2), cette mer étant, réitère Ptolémée quand il s’agit d’énumérer les mers “incluses dans notre monde habité”, “entièrement encerclée par la terre” (VII, 5, 3-4) fait évidemment sens pour nous, Réunionnais (qui nous sentons parfois “au sud, très au sud du monde”, comme écrivaient les Leblond), immédiatement concernés par cette “antichtonie”. Selon Ptolémée, la Lybie touche à l’Asie par “la terre inconnue qui enserre la mer de l’Inde” (VII, 5, 5). Sauf sur sa façade occidentale, le monde habité serait partout prolongé par des terres inconnues. Pour ce qui concerne la conjecture australe, je renvoie aux travaux de notre collègue Jean-Michel Racault sur le mythe austral, qui continuera de prospérer jusqu'aux expéditions de James Cook, entre 1768 et 1775 (voir aussi : Numa Broc, “de l’Antichtone à l’Antarctique”, dans Cartes et figures de la terre, 1980). (Cette postulation est en réalité cohérente avec la théorie des sphères et celle de la gravité : les pythagoriciens, au Ve siècle, avaient formé l’idée d'un continent austral en relation avec la rotondité de la terre ; Cratès de Mallos, au IIe siècle avant l’ère chrétienne, représentait le monde composé de quatre masses continentales : deux au Sud, et deux au Nord, le monde connu occupant le quadrant nord-est). Comme l’exprime la représentation du globe illustrant la traduction latine de sa Géographie par Jacobo d’Angelo (vide infra), Ptolémée donne à penser le monde habité comme une large “pelure” – qui va du parallèle de Thulé jusqu’au parallèle d’Anti-Méroé – enveloppant le globe. Ayant perfectionné un système de coordonnées et de projections permettant de déterminer tous les points de la sphère et d’en figurer les positions, y ayant porté les limites extrêmes du monde connu et figuré la terre inconnue, il prépare les esprits à la découverte et trace les routes virtuelles du futur.
Le Zodiaque sur le bouclier d'Achille :
Elisabeth-Sophie Chéron, Pierres Antiques gravées tirées des principaux cabinets de France. Paris, 1711.
(BnF, Monnaies et Médailles (Res 54100 Che fol.)

Le Bouclier d'Achille, Iliade, livre XVIII. L'univers est symbolisé par le Zodiaque.
A chacun des douze signes zodiacaux correspond une scène de la vie d'Achille.
Le monde d'Homère :
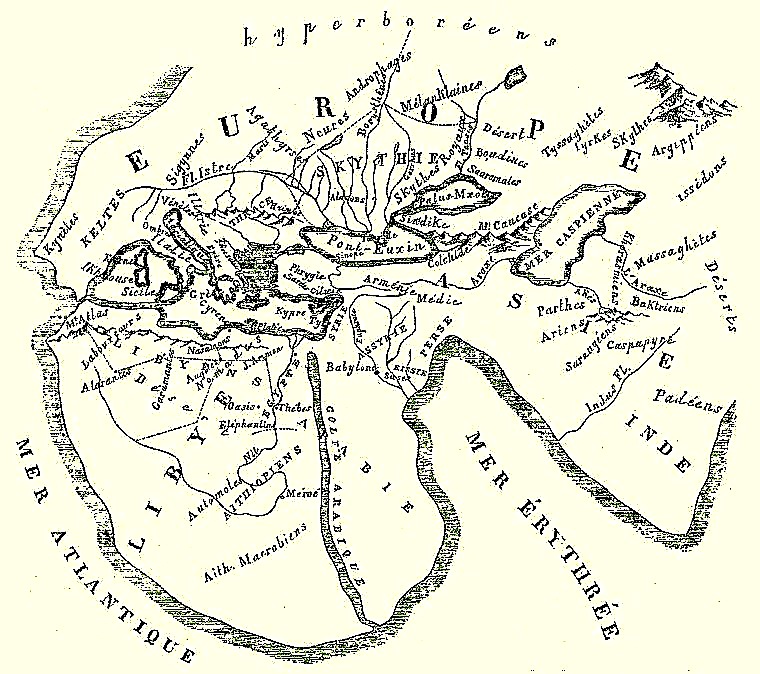
Carte dessinée par Mary O. MacCarthy (1849)
Carte d'Ératosthène :
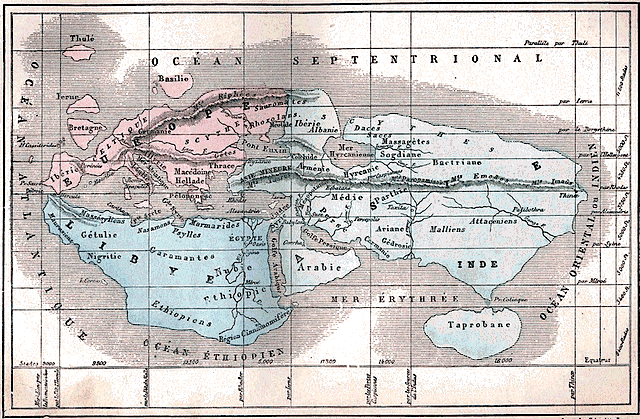
Dans : A. Villemin dans La Terre et les mers, ou description physique du globe,
de L. Figuier, Paris, Librairie Hachette, 1884
La terre selon Posidonius :
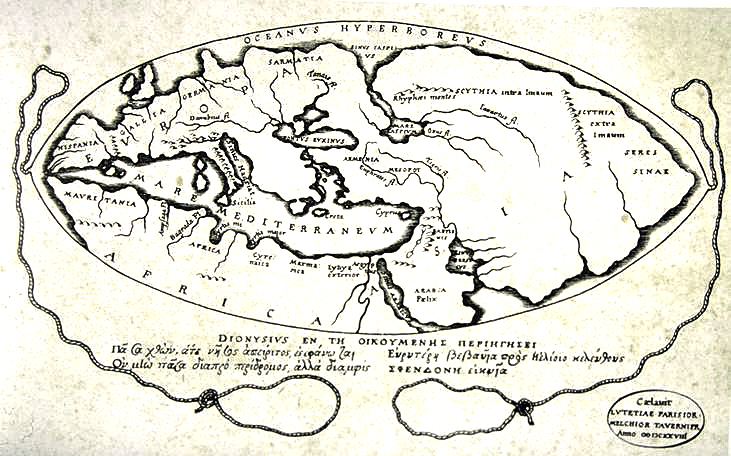
La terre selon Ptolémée :
Traduction latine de Jacopo d'Angelo de la Cosmographia (Géographie, de Ptolémée)
Florence, vers 1465-1470
Manuscrit sur parchemin (48 x 40 cm). BnF, Manuscrits (Latin 4801 fol. 74)

Cosmographie, publiée à Ulm en 1482
L. Holle, 1482
cote: Inc. C 94 LP
Mappemonde “gravée par John Schnitzer de Arnheim” (l. 1)
(Représentation du Nil, de ses différents bras et de ses sources dans les “Monts de la Lune”)
Reproduction issue du site web de la Bibliothèque Royale de Belgique : http://www.kbr.be/america/fr/fr1.htm
avec le commentaire suivant (adapté) :
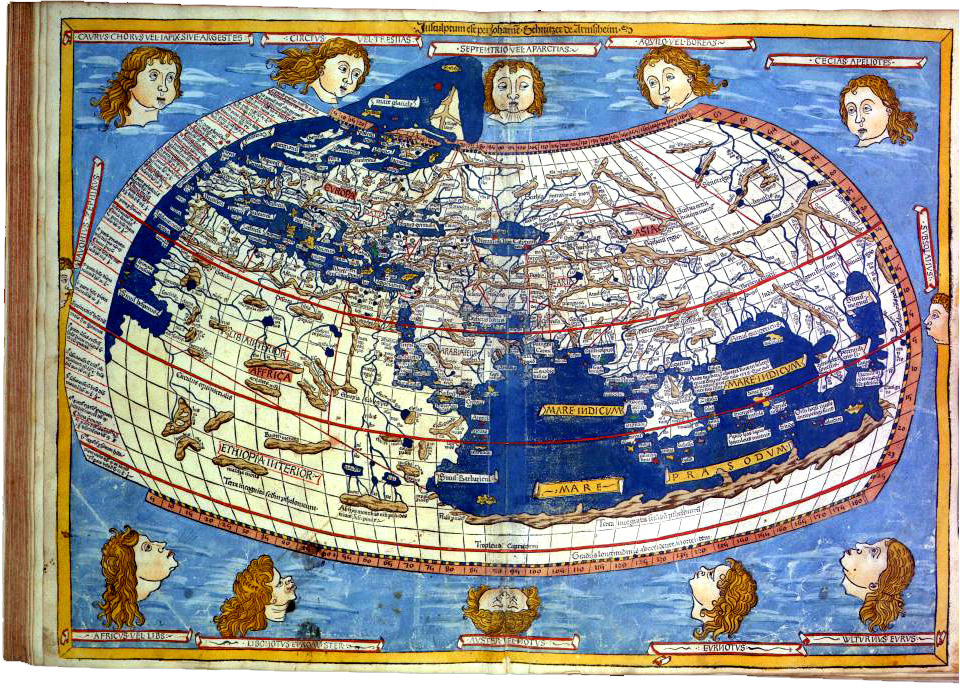
L’édition d’Ulm de la Cosmographia a été réalisée par le bénédictin Nicholas Germanus, cartographe et enlumineur qui offre au duc de Ferrare, en 1466, une carte qu’il a dressée à partir de la Géographie. Une copie est imprimée à Bologne en 1477. L’édition d’Ulm est imprimée par Leinhart Holle à partir du manuscrit de Germanus. Une deuxième édition fut publiée également à Ulm en 1486. L’édition de 1482 contient trente-deux cartes gravées sur bois. Comme dans les éditions antérieures, par exemple celle de Rome en 1478, ou celle due à Berlinghieri en 1462, les cartes de l’édition de 1482 sont tracées selon la nouvelle projection avec des méridiens et des parallèles courbes. Si on la compare avec la réédition de Berlinghieri (Florence, ca 1480) l’édition d'Ulm contient cinq nouvelles cartes, dont une du Nord de l’Europe qui englobe le Groenland, fait qui fut considéré comme une preuve de la connaissance du Nouveau Monde avant la découverte de Colomb. [...] Erasme édita à Bâle, en 1533, la version originale de la Cosmographia. C’est la première édition du texte grec. Les cartes qui sont jointes à l’ouvrage de Ptolémée, aussi bien dans les différents textes manuscrits que dans les éditions, sont l’œuvre d’Agathodémon (Vème siècle), ingénieur et mécanicien d’Alexandrie.

"VNIVERSALIS COSMOGRAPHIA SECVNDVM PTHOLOMAEI TRADITIONEM ET AMERICI VESPVCII ALIORVQUE LVSTRATIONES",
Planisphère dû à Martin Waldseemüller qui, en 1507, attribue le nom d'Americo Vespucci au continent nouvellement découvert (voir grossissement).
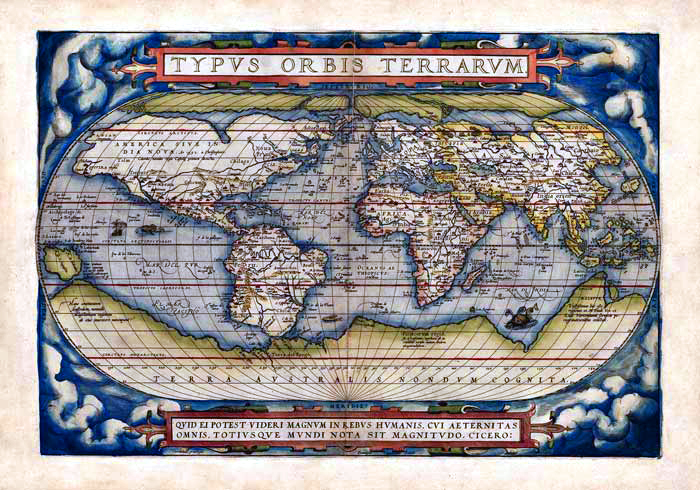
La terre australe, selon Ortelius :
ce “continent austral que plus d’un nomment pays de Magellan, d’après son inventeur” (Ortelius),
ORTELIUS, Abraham
Typvs Orbis Terrarvm
Antwerp, 1595, Latin text edition. 360 x 495
source : www.tooleys.co.uk/a8.htm
“...et retournant à l'autre pole du Sur, il n'y a pas homme qui sçache où s'arreste la terre qui est de l'austre costé du detroit de Magellan.”
(traduction française, parue en 1598, de l'Historia natural y moral de las Indias, du jésuite José de Acosta, publiée à Séville en 1590, f° 41 v°)
*
Que Ptolémée, redécouvert et traduit en latin à la Renaissance, pionnier ou fédérateur de la science de son temps, soit devenu le rempart du dogme avec sa théorie géocentrique, voilà aussi qui nous rappelle le caractère spécifique de la recherche scientifique : quand les dogmes sont aussi merveilleux qu’intangibles, la science est toujours en chantier. C’est une leçon de l’antiquité, que cette “journée” nous donne l’occasion de méditer : la concurrence des savoirs, la concurrence plus précisément entre les visions anthropocentriques du monde – les dogmes – et le savoir objectif.
Pour l'iconographie de Ptolémée :
http://www.er.uqam.ca/nobel/r14310/Ptolemy/index.html
(Communication présentée à la “Journée de l’Antiquité”, Université de la Réunion, 27 avril 2005)
Plan du chapitre :
A) Le territoire de la langue : les deux natures
Communication présentée au colloque international Langues et droits, Université de Paris X-Nanterre, 22-23-24 octobre 1998.
B) La mesure du monde : Eratosthène et Ptolémée
Communication présentée à la “Journée de l’Antiquité”, Université de la Réunion, 27 avril 2005.
C) “Deux vérités ne peuvent être contraires" (Galilée) (en cours)
D) “Foi d'animal” : vérité du bestiaire dans la fable et le conte
Communication présentée aux “Journées de la Recherche” du CRLHOI, séance du 11 février 2006.
|
|
|